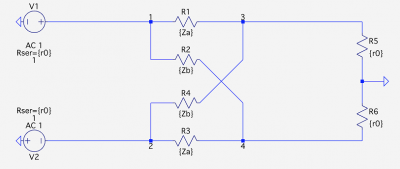
Балансный регулятор типа решетка
Плюсы:
- Простой
- Симметричный (вход и выход, верх и низ)
- Постоянное входное и выходное сопротивление на всех шагах громкости
- Всего 2 пары перекидных контактов на 1 ступеньку
- Хорошо симулируется
http://forum.vegalab.ru/showthread.php?t=84271&p=2600445&viewfull=1#post2600445
Excel-файл для расчета:
lattice_rg_.xls
Там вроде как понятно.
Красным - то, что нужно ввести.
1. Величину шага громкости;
2. Сопротивление источника и нагрузочное (основное - нагрузочное, под него все строится, сопротивление источника должно быть таким-же, но на практике бывает всяко);
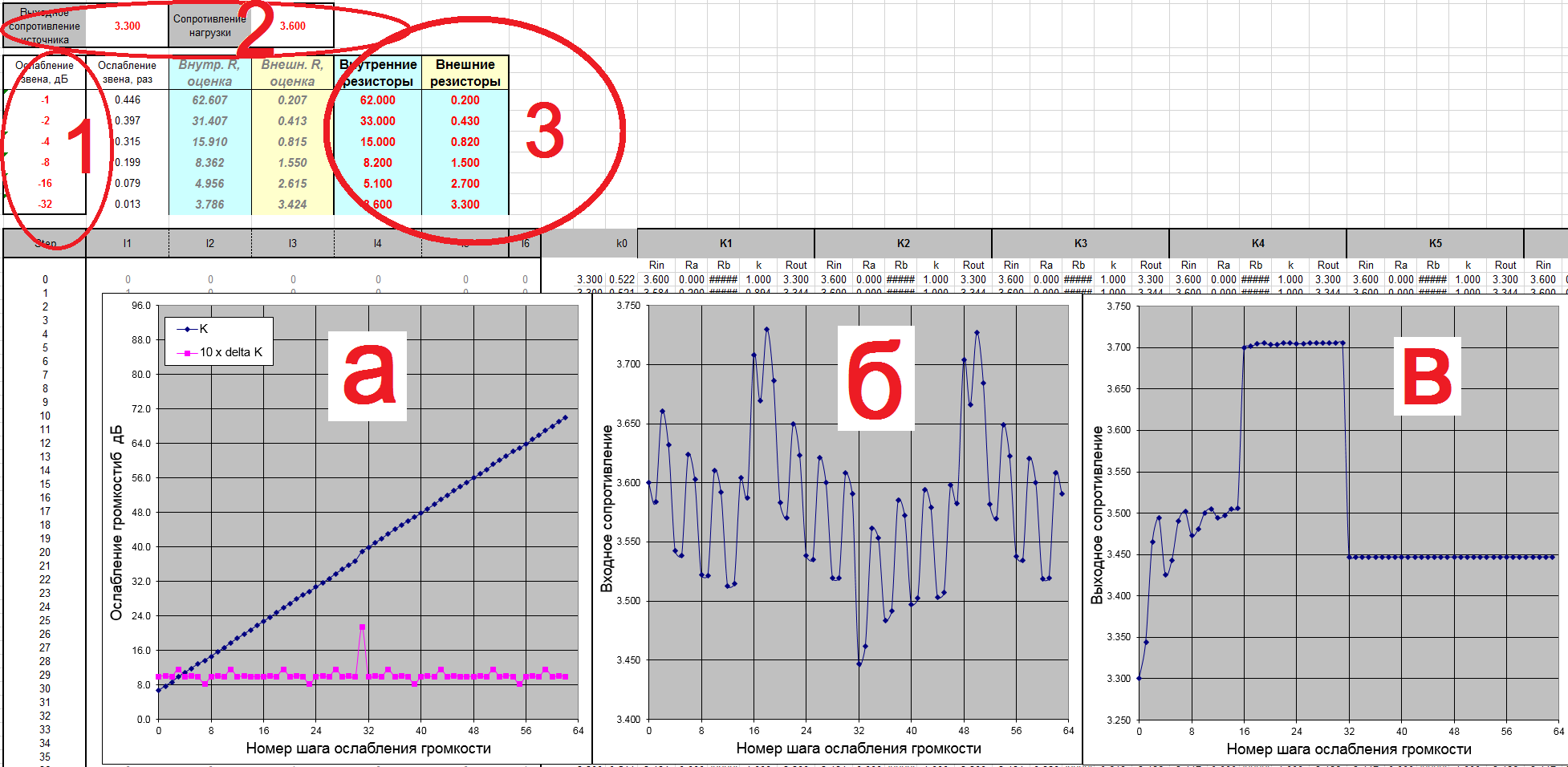
3. Номиналы резисторов в звеньях. Серым чуть левее - прикидочные идеальные значения (они считаются автоматом).
Нужно вбить реальные номиналы резисторов (из доступных) и посмотреть на графиках, что получается
а) в плане равномерности регулировки (шкала ослабления от номера шага + удесятеренный шаг (видна неравномерность шагов));
б) в плане входного сопротивления;
в) выходного сопротивления.
Пример намеренно условный. Например, сопротивление источника выбрано немного другим, да резисторы подобраны преувеличенно грубо, в основном, чтобы проиллюстрировать, как те или иные неточности себя проявляют.
По опыту с обычным РГ, порой получается легко уложиться хоть и в ряд номиналов E12, если чуть поиграть размером ступени (не точно 1.0/1.5 дБ, а например 1.07 дБ) или выбранным нагрузочным сопротивлением (скажем не 2 кОм, а 2.1 кОм).
Примечание. В данном РГ сложно добиться нормальной точности с обычными резисторами на последней ступени при ее больших ослаблениях (например, 40 дБ и больше). Получается, что в таком случае на плате стоит сделать «внутренние» резисторы сдвоенными - как последовательное включение одного с номиналом как у «внешнего», и второго, небольшого номинала, который и будет определять реальное ослабление.